The Pure Theory of Multinational Enterprises (MNE)

Copyright: JGANDER, 1999

The theory explains the size of the MNE in terms of its Home (H) activities and its host (h) or subsidiary activities. The approach is heuristic and an adapatation from Coase's model of the firm. H is some metric index of size reflecting a set of activities (like, procurement, production, marketing and advertisement, finance, and research and development). The same definition applies to the metric h for the subsidiary. I assume they are continuous and can be added. After the theory, I operationalize the H and h and present an index of globalization and global intensity.

The MNE has the following profit function

where P is profit, A is the efficiency parameter for advertising activity and when it increases the effectiveness of a given amount of advertisement on product demand and revenue increases, R is the efficiency parameter for RND activity and when it increases the output (new products and/or processes) from RND also increases, D represents the parameter for inter-firm coordination and when it increases the rival firms in a given product market are behaving more cooperatively, V is the net value of the level of the activities (in effect, revenue minus cost), and C represents the internal transaction costs of the activities the MNE is coordinating.

The profit-maximizing equilibrium conditions (marginal rules) are

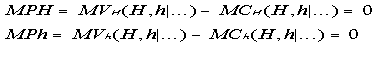
where MPH and MPh are the marginal profit functions set equal to zero and solved jointly for H and h. The marginal values are decreasing in H and h, respectively. The marginal costs are assumed to be constant for simplicity in H and h, respectively, independent of the three parameters, and independent of each other, but interactions could be brought in and economies of scale or diseconomies of scale could be assumed. I further assume that technical complementarity exists for H and h, so that MVH increases when h increases and MVh increases when H increases. The A and R positively affect MVH and MVh. The parameter D is complicated to handle. Essentially, if competition in the industry increases so that D decreases, then MVH and MVh are negatively affected.

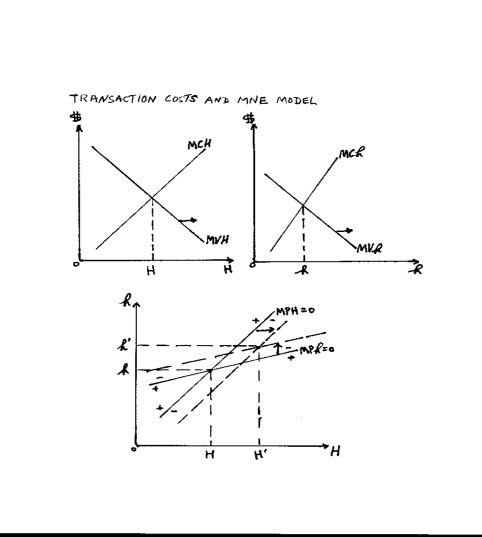
The two graphs of the marginal rules are shown below. The two rules can also be graphed as two equations, MPH(H,h)=0 and MPh(H,h)=0, in H and h, with H on the horizontal axis and MPH steeper in slope than Mph. The equilibrium is given by the intersection of the two functions. For our assumptions and purposes, the joint equilibrium is stable as indicated by the + and - signs in the phase diagram also given below.

In either set of graphs, an increase in A or R parameters will result in shifts of the curves. In the top two graphs, MVH and Mvh shift right and in the phase graph MPH shifts right and MPh shifts vertically, resulting in a new joint equilibrium with H and h larger. The ratio of h/H is an index of globalization and operationalized by the ratio of foreign sales/domestic sales. Alternatively, the ratio of h/H+h) is the globalization intensity index and operationalized by the ratio of foreign sales/total sales, for the MNE. Either index can then be regressed on the A and R and other variables.